According to the put-call parity concept, there is a fixed link between the time premium of puts and calls that is determined by the options’ volatility and the risk-free interest rate. The idea is intriguing, but retail traders rarely pay much attention to it because its details can seem complex and impractical — relevant only to theory geeks and floor traders who pay miniscule transaction costs. But if you understand the simple equation behind putcall parity, it may change the way you trade certain positions. This formula provides flexibility, because it shows there are two ways to create any options position. For example, if you are bullish on a company, you can either buy its stock or buy a call and sell a put simultaneously (“synthetic stock”), which theoretically offers the same risks and rewards — often with a lower capital requirement. The following four sets of equivalent option positions illustrate how to use put-call parity to find the most practical positions to trade. The put-call parity equation The put-call parity equation states that the value (and therefore the time premium) of puts and calls with the same expiration date and the same strike price is linked. In its simplest form the formula is:
T-bill = Stock – call + put
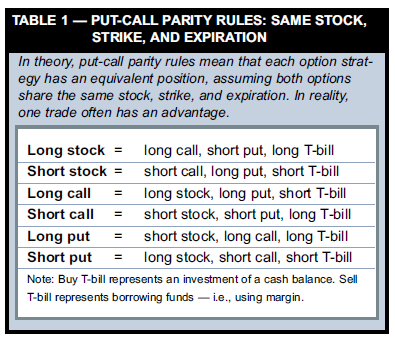
This means if you purchase a stock and sell a call and buy a put with the same expiration date and strike price, your position will have the same potential risk and return of a Treasury bill. What’s the big deal? Anyone who wants a T-bill should simply buy one instead of trying to clone it by executing three trades and paying three commissions. However, the practical aspects of this formula appear when you rearrange its elements. Table 1 summarizes several position equivalents using put-call parity.
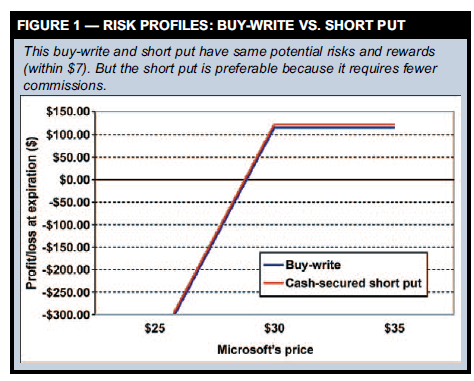
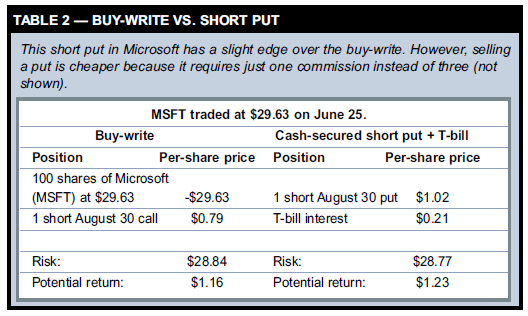
Buy-write vs. cash-secured short put Two familiar option strategies emerge if you subtract the put from both sides of the formula: Stock – call = -Put + T-bill The left side of the equation represents a buy-write, or covered call (long stock and short call), and the right side represents a “cash-secured” short put — two positions that are often considered equivalent. Let’s test this theory with a recent example. On June 25 Microsoft (MSFT) traded at $29.63, the August 30 call was at $0.79, and the August 30 put was at $1.02. Which strategy is better — a buy-write (long 100 shares, short call) or a short put? (The two strategies must share the same expiration date and strike price or you’ll be comparing apples to oranges.) First we need to find the potential return and risk of both strategies. Table 2 shows each trade’s components and Figure 1 shows each position’s profits and losses at expiration on Aug. 18. Both positions reach their maximum profits if MSFT trades above $30 at expiration. The buy-write will gain a total of $1.16 ($0.37 from the stock + $0.79 call premium). The short 30 put will gain $1.23 overall. You keep its premium ($1.02), plus the interest earned on a T-bill ($0.21, assuming five-percent interest for 53 days). The risk of both strategies is stock ownership. The buy-write represents a long stock position with a net cost of $28.84 ($29.63 stock price – $0.79 premium). If the short put is assigned, you will hold 100 shares of Microsoft at a net cost of $28.77 ($30 strike – $1.02 premium – $0.21 interest). Both strategies offer the same potential rewards and risks, give or take $0.07. Why favor one strategy over the other? The answer is real-life costs. Putcall parity assumes no transaction costs. However, trading a buy-write requires two commissions even in the best-case scenario. To enter the trade, you must buy 100 shares of Microsoft and sell a call. If MSFT is above $30 and the shares are called away by the call’s owner, you must then pay a third commission upon assignment. By contrast, you pay only one commission when you sell a cash-secured put. In the best-case scenario the short put expires worthless. In reality, selling a put seems preferable to a buywrite.
Comparing vertical spreads You can use the original put-call parity equation to find comparable options positions. To find the equivalent to a vertical debit spread, let’s start with a long 85 call: Call85 = + put85 + stock – T-bill
Then, find the alternative to a short 95 call: -Call95 = – put95 – stock + T-bill
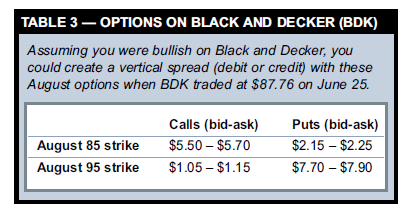
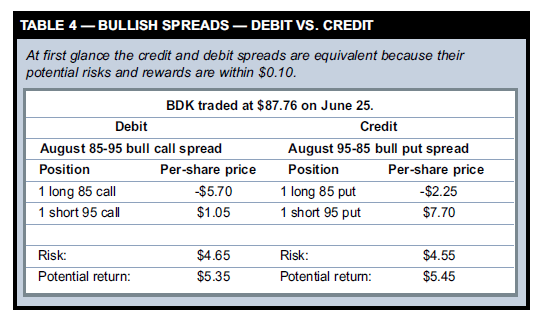
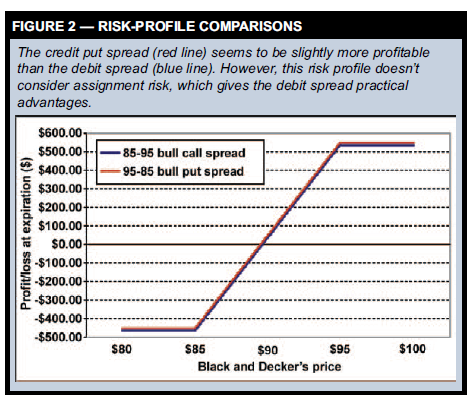
Next, combine a long 85 call with a short 95 call to create an 85-95 bull call debit spread: Call85 – call95 = + put85 – put95 + stock – stock + T-bill – T-bill Finally, the answer appears after you simplify the right side of the equation: Call85 – call95 = + put85 – put95 This formula means an 85-95 bull call spread should equal a 95-85 bull put spread. Let’s check this with a trade example. Table 3 shows August option prices for Black & Decker (BDK) when it traded at $87.76 on June 25. To enter an 85-95 bull call spread, you would buy an 85 call at $5.70 and sell a 95 call at $1.05 — an initial net debit of $4.65. To construct the equivalent 95-85 bull put spread, sell a 95 put at $7.70 and buy an 85 put at $2.25 for an initial credit of $5.45. Table 4 shows both strategies’ potential risk and profit. Figure 2 compares their risk profiles at expiration. Once again, the strategies are equivalent (within $0.10). In this case it’s more difficult to argue one position has higher transaction costs than the other. However, the put-call parity equation assumes options are European-style, which means option holders can’t exercise them early. This may be true for most index options, but not for equity options.
Exercise and assignment
How does early exercise or assignment affect the spreads? In the 85-95 bull call spread, the short 95 call will only be assigned if BDK rises above $95. If this happens, exercise the long 85 call. If you are assigned by the short call’s owner, you will be forced to sell BDK at $95. Exercising the 85 call will close the spread by purchasing BDK at $85, effectively capturing its $10 maximum value for a profit of $5.35 ($10 – $4.65 debit). In the 95-85 bull put spread, the short 95 put could be assigned whenever BDK trades below $95. If this happens, you will be forced to buy shares from the put holder at $95. Unlike the debit spread there is no clear next step. If BDK falls below $85 you could exercise the long 85 put, sell those shares, and exit the trade. But BDK could be trading between $95 and $85. In this case, it does not make sense to exercise the long 85 put, because you can sell BDK shares at a higher price. Also, if the short 95 put is assigned, the resulting position includes BDK shares and a long 85 put — something quite different from the original spread (with a much higher capital requirement).
The debit vs. credit debate
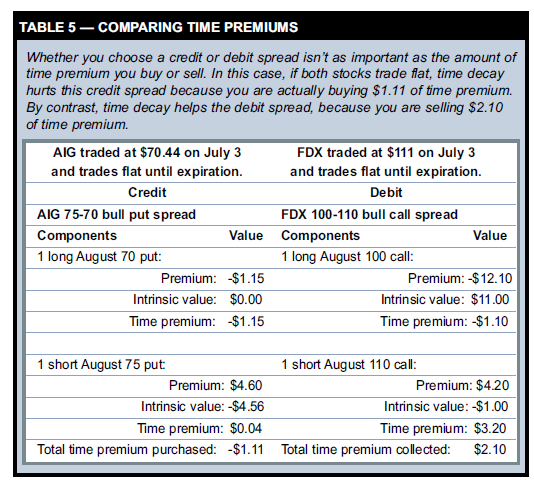
So far debit spreads seem preferable to credit spreads, at least for stock and Americanstyle index options. But aren’t credit spreads better because they benefit from time decay while debit spreads suffer from it? Not necessarily. Whether you choose a credit or debit spread isn’t as important as the amount of time premium you buy or sell. To explain this, let’s compare two more spreads. On July 3, American International Group (AIG) traded at $70.44. To construct a bull put spread, you could have sold an August 75 put for $4.60 and bought an August 70 put at $1.15 — a credit of $3.45. If AIG trades sideways in the 45 days until expiration, this spread’s value will slowly increase from $3.45 to $4.56, bad news for a spread “seller” who is now feeling the negative impact of time decay. And debit spreads can benefit from time decay. On July 3, Federal Express (FDX) traded at $111.00. To create a bull call spread, you could have bought an August 100 call at $12.10 and sold an August 110 call for $4.20 — a debit of $7.90. Assuming FDX remains at $111 until Aug. 18 expiration, this 100-110 call spread’s value will slowly increase from $7.90 to $10 as it takes advantage of the calls’ time decay. What’s happening here? In the AIG credit spread, the long 70 put had $1.15 in time premium, and the short 75 put only had $0.04 of time premium. When you buy more time premium than you sell, time decay works against you. In the FDX debit spread, the long 100 call had $1.10 of time premium, and the short 110 call had $3.20 of time value. When you buy the 100-110 call spread, you are actually selling $2.10 of time premium. Table 5 shows both spread’s components and highlights each option’s time premium.
Selling short vs. long put
Let’s assume you decided to sell short 100 shares of Apple Inc. (AAPL) when it traded at $123.87 on June 19. Because selling short is a high-risk strategy, you also choose to buy a September 130 call at $6.00 as a hedge. The bearish position limits upside risk and offers potential profit if AAPL heads south by Sept. 15 expiration. Next, check the put-call parity equation to find the equivalent strategy: Put = -Stock + call + T-bill
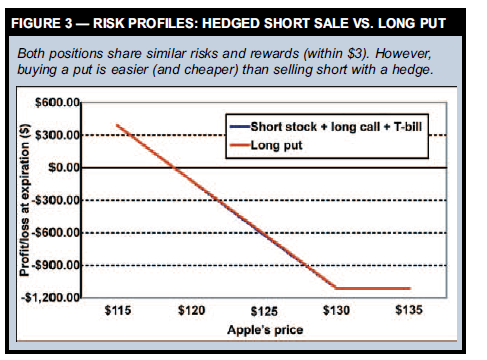
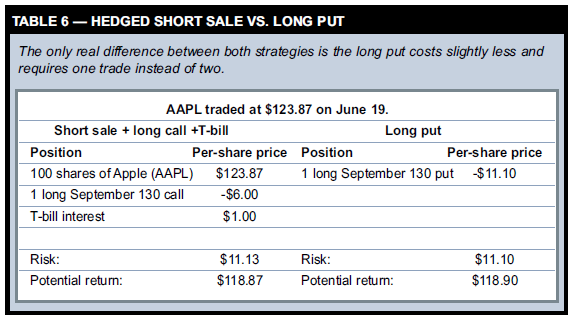
A long put also has limited risk and will be profitable if the underlying stock declines by a sufficient amount. However, a long put has two advantages over the first strategy: You don’t have to borrow shares, and transaction costs are lower (one trade instead of two). On June 19, you could have bought a September 130 put for $11.10, which also represents its total risk. By contrast, the risk of the shortstock, long-call position is $12.13 ($130 strike – $123.87 entry price + $6 call premium). At first glance, the combined strategy’s risk appears higher. But the T-bill’s interest from the equation hasn’t been included yet. Remember, if you sell a stock short, your broker might let you invest that capital in a risk-free instrument such as T-bills. If you can invest the cash it will generate $1.00 of interest, assuming the short sale’s proceeds ($123.87) are invested at 5 percent for 59 days. That interest reduces the stock-call-T-bill position’s risk to $11.13, virtually the same as the long put. Table 6 compares both trades’ risks and rewards and Figure 3 shows their potential gains and losses at Sept. 15 expiration. Basically, both strategies behave the same. The long put costs $0.03 less and requires only one trade, which are the only practical differences.
Keeping it real
In a world of European-style options without transaction costs, options traders would be completely indifferent to comparable positions determined by the put-call parity equation. But reality gets in the way, and understanding put-call parity can point you to toward the more advantageous of two seemingly equivalent strategies.